Blog
-
Three new papers for Autumn/Winter 2019
It’s been a productive summer/fall, and as a result we have three new papers published/in submission.
Buffer Sizing and Video QoE Measurements at Netflix
I spent the summer working at Netflix, doing measurements related to how the sizes of router buffers affect video performance. We learned a whole bunch of stuff about how routers work, and this was the result.
This is a classic networking area that my advisor Nick has done a lot of work in. When too many packets are sent to a router at once, the router puts them in a buffer so that it can send them later when it gets a chance. If the buffer is full, it throws away the packets. The question is, what size should the buffer be? Too large and maybe packets wait around a long time to be sent. Too small and maybe too many packets get thrown away.
In this work, we basically set up a nice, controlled experiment and tried a bunch of different router buffer sizes and observed what happened. We found all kinds of weird things, like queues which never drained, TCP going truly wild with large queueing delay, and buggy router scheduling algorithms. Check it out!
Coded Trace reconstruction in a constant number of traces
This paper was a fun side project with Ray and Josh. We have a coding theory reading group, and last fall I presented some papers on trace reconstruction. Trace reconstruction is this cool problem where you get independent, random substrings of some initial string and the goal is to recover the initial string. For instance, maybe the string is “wow cool paper” and the random traces you get are “ww cool ppr,” “wow cool,” and “cool paper,” which together let you figure out the initial string.
In the spring we read this very interesting paper on Coded Trace Reconstruction. In regular trace reconstruction, the string is either (1) any string or (2) a uniformly random string, and there’s this huge exponential gap between the best known upper and lower bounds for both. The exciting thing to us about this Coded Trace Reconstruction paper is that it beat the number of traces required for a uniformly random string. We were curious how far we could push this idea.
We wound up showing a couple very cool results:
- We give a construction of high rate, binary codes that can recover the initial string from a constant number of traces. It’s kinda surprising that this is possible, since even the random string case requires some polylogarithmic number of traces.
- We show theorems which take upper and lower bounds for trace reconstruction and turn them, in a black-box way, into a construction for coded trace reconstruction.
- We show that if you are a bit generous and give us a constant sized alphabet instead of a binary alphabet, we can get matching upper and lower bounds for coded trace reconstruction. I found this particularly exciting because usually there’s this horrible exponential gap in any trace reconstruction problem, and here we were able to avoid that.
The paper is on arXiv
On estimating the number of flows
This is a little paper we wrote for the Stanford Buffer Sizing Workshop. There’s a bunch of existing work that says the size of a router buffer depends on the number of flows using that buffer. Unfortunately, none of the work says how to figure out the number of flows using a router. It turns out to be not easy, and we spent some time thinking about definitions, how to estimate those definitions, and what this means in practice. I think the conclusion is that if you design a new congestion control algorithm, it would save everyone a lot of trouble if you could make it so the buffer requirements didn’t depend on the number of flows, whatever that means.
-
New paper: Unconstraining graph-constrained group testing
We just submitted a new paper on Graph-Constrained Group Testing which I’m really excited about!
The problem we consider is related to debugging networks: suppose you have a network where some of the links in your network fail. You can send a packet around the network, and observe whether it reaches its destination or not. How many packets do you need to send to find the failing links?
This is my blog, so here’s a bonus version of the problem. Suppose you manage a large national park with lots of hiking trails. Last night there was a huge storm, and a few trails (at most $d$) have been washed out. You would like to know which trails were washed out before you reopen the park, so that you can warn visitors. The catch is that in this universe, the only way you can tell if a trail has been washed out is to hire a hiker and send them on some walk around the park. If the hiker comes back, you know every trail they visited was good. However, if they find a washed out trail, they’ll lose the trail and wander around the woods for a bit, so you know that some trail they visited was bad. You could send out hikers one by one and wait for them to get back, but hey, you have a park to open here! The question is: what is the minimum number of hikers you need to send out simultaneously to find all the washed out trails?
Here’s the more formal version of this problem. You have a graph $G = (V,E)$ where $|V| = n, |E| = m$ and some set $B \subseteq E$ of the edges are defective. $B$ is a small set, of size at most $d$. You can test some connected subgraph $G’$ of $G$ and determine whether any edge in $B$ is in $G’$. The problem is to find the minimum number of non-adaptive tests such that $B$ can be exactly identified from the test results.
If there were no graph in this problem, this would be a classic problem called Combinatorial Group Testing. During World War II, the military was interested in finding soldiers with syphilis using some blood test. Syphilis tests were very expensive, and the military didn’t want to test everyone individually. In a nice paper from 1948, Dorfman showed that by testing groups (i.e. mix a bunch of blood in a bucket and test the bucket), one could find the sick soldiers using many fewer tests.
Group testing (sans graph constraints) can be solved using roughly $O(d^2 \log m)$ tests. With the graph constraints, the answer is less well-known. [Harvey 2007] gave the answer for a number of special cases, and showed that roughly $O(d^3 \log m)$ tests were enough for certain graphs. In a later work, [Cheraghchi 2010] showed a cool algorithm using random walks which uses roughly $O(d^2 \text{polylog } m)$ tests for good expanders and, surprisingly, $O(d^2 \log m)$ tests for a complete graph. That is, group testing with the constraints added by the complete graph is in some sense no more difficult than group testing without constraints.
We show the following result: for many graphs, you can do group testing in only $O(d^2 \log m)$ tests! As long as the graph is sufficiently well-connected, you can do group testing with graph constraints “for free.” The graphs this works for includes complete graphs, good expanders (e.g. random regular graphs and Erdos-Renyi graphs), and graphs which are “clusters” of good expanders (e.g. a barbell).
There’s also a cool technical result about “giant components” of graphs. Suppose you have a graph, and sparsify it by constructing a subgraph which includes each edge independently with probability $p$. What does this subgraph look like? For the complete graph, this question was studied by Erdős and Rényi in the 50s, and it turns out that a “giant component” - a connected component which includes lots of nodes - appears at a certain threshold. For $p=\frac{1-\epsilon}{n}$, the largest connected component has size $O(\log n)$. For $p = \frac{1+\epsilon}{n}$, the largest has size $O(n)$. It turns out (and has been known for a while) the same thing happens in expander graphs. We prove a slightly stronger version of this result about expanders, which was helpful in analyzing our algorithm. You can check out the paper for the full details, but for now let me just show some neat pictures of giant components:
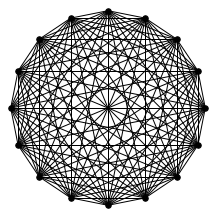
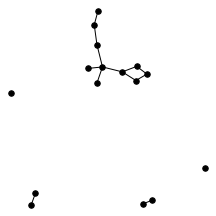
A complete graph on 16 nodes on the left, and sparsified with probability $\frac{1 + 0.2}{16}$ on the right. 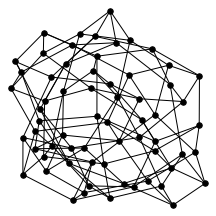
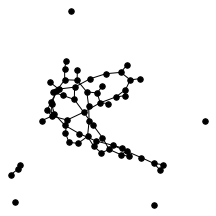
A random regular graph (left) and sparsified (right). 
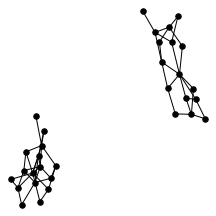
A barbell graph (left) has two giant components (right) when sparsified. -
Optimal Gambling at Stardew Valley's Roulette Wheel

I’ve been playing a bit of Stardew Valley recently. At some point you go to the Stardew Valley Fair, where there’s a roulette wheel you can play which comes up green with probability $3/4$ and orange with probability $1/4$. Winning gives you star tokens, and there’s big incentive to get lots of stars: you can win a rare scarecrow! Betting on a roulette wheel biased in our favor seems like a great way to get them.
In this post, I’ll show that the optimal strategy is to bet half your stars on green in each round.
The only thing standing between us and the rare scarecrow of our dreams is finding the optimal way to bet on this wheel. Obviously we don’t want to bet all our stars on green, since there’s some decent probability we’d lose everything. On the other hand, if we bet just one star each time, we would win an average of 1.5 stars for each star we bet, and if we played long enough we’d be sure to make money. But this is so slow! I’m a busy grad student! I can’t spend all this time gambling, so instead, let’s blow an afternoon proving what the optimal strategy is using martingales.
There are many options for defining an optimal strategy, but since it only takes 800 stars to win the rare scarecrow, we’ll say the optimal strategy minimizes the expected time it takes to reach 800 stars. We’ll prove that the optimal strategy is to bet half your stars each round.
More formally, let $X_n$ be the number of stars we have at round $n$, $\gamma$ the fraction of $X_n$ we bet, $\{Y_n\}_{n=0}^\infty$ be independent and identically distributed random variables where $Y_n = 1$ with probability $p$ and $Y_n = -1$ with probability $1-p$. Then, \(X_{n+1} = X_n + \gamma Y_n X_n = X_n(1+\gamma Y_n).\)
Let $T_a$ be the first round we have more than $a$ stars, or formally, $T_a = \inf\{n : X_n \geq a\}.$ We prove the following result, which happens to be a variation of the Kelly Criterion,
Theorem. In the above setting, $\E T_a$ is minimized if $\gamma = 2p-1.$
Proof. Let $S_n = \log X_n = \sum_{i=1}^n \log(1+\gamma Y_i)$. Define $\beta = (p\log(1+\gamma) + (1-p)\log(1-\gamma))$, so that $Z_n = S_n - \beta n$. $Z_n$ is a martingale with respect to $F_n = \sigma(X_0, Y_1, \ldots, Y_n)$ since, \(\begin{align*} \E[Z_n | F_{n-1}] &= S_{n-1} + \E[\log(1+\gamma Y_i)] - \beta(n-1) - \beta,\\ &= S_{n-1} + p\log(1+\gamma)+(1-p)\log(1-\gamma) - \beta(n-1) - \beta,\\ &= S_{n-1} - \beta(n-1). \end{align*}\)
Applying the Optional Stopping Theorem, since $|(S_n - \beta n) - (S_{n-1} - \beta (n - 1))| \leq |\log(1+\gamma) - \beta|$ which is a constant, \(\begin{align*} Z_0 &= \E[Z_{T_a}],\\ \log(X_0) &= \E[ S_{T_a} - \beta T_a],\\ &= \log(a) - \beta \E T_a,\\ \E T_a &= \frac{\log(a) - \log(X_0)}{\beta}. \end{align*}\)
It remains to show that $\beta$ is maximized by $\gamma = 1/2$, but this follows since \(\frac{d}{d\gamma} \beta = \frac{1+\gamma-2p}{\gamma^2-1},\) Setting $\frac{d}{d\gamma} \beta = 0$ yields \(\gamma = 2p-1.\) $\square$
-
Some Updates
Hey pals,
I’ve been silent on social media for a few months now, so I figured I’d write something up about what I’ve been up to.
Next week, I’m presenting our paper “MON: Mission-optimized Overlay Networks” (my first paper!!) at INFOCOM in Atlanta. We looked at designing an overlay network which optimally routes traffic. There’s a tradeoff with these systems between a centralized system which solves the problem exactly but is not very resilient, and a distributed system which solves the problem inexactly but which is reliable and responds quickly to changes. We propose what I think is a very cool two-layer architecture. It uses some TCP trickery to combine the strengths of both the centralized and distributed systems. Check out the paper on arXiv
The week after next, I’m graduating from UMass with my Master’s in computer science. I’m working on a thesis about estimating the capacity of a network using TCP measurements. I’ve submitted a short version of it to the MAMA workshop and will share the thesis as soon as I finish writing it.
In September, I’m moving to Palo Alto and starting a PhD at Stanford! If you live in the Bay Area, hopefully I will see more of you!